En las pruebas de diferencia, el desempeño de los jueces varía en función de la prueba utilizada. Esta diferencia se explica a partir del conocimiento sobre la forma en que el cerebro procesa la información que recibe de los sentidos, particularmente el sentido del gusto. En algunas pruebas de diferencia, la información se procesa de manera más eficiente que en otras. El modelo de Thurstone describe las estrategias del cerebro para procesar la información en función del método utilizado. Esta revisión introduce las ideas y los conceptos de este modelo en las mediciones sensoriales derivadas con las pruebas de diferencia. Los conceptos de la variabilidad del estímulo y la estrategia cognitiva correspondiente a cada método de diferencia son la base para el cálculo de la magnitud de la diferencia percibida entre dos estímulos, denominada d’. Esta medición es fundamental e independiente de la metodología sensorial utilizada.
Palabras clave: Evaluación sensorial, pruebas de diferencia, modelo Thurstoniano, teoría de detección de señales, estrategias cognitivas.
Part of understanding why judges perform better on some difference tests than others requires an understanding of how information coming from the mouth to the brain is processed. For some tests it is processed more efficiently than others. This is described by what has been called Thurstonian modeling. This brief review introduces the concepts and ideas involved in Thurstonian modeling as applied to sensory difference measurement. It summarizes the literature concerned with the theorizing and confirmation of Thurstonian models. It introduces the important concept of stimulus variability and the fundamental measure of sensory difference: d’. It indicates how the paradox of discriminatory non-discriminators, which had puzzled researchers for years, can be simply explained using the model. It considers how memory effects and the complex interactions in the mouth can reduce d’ by increasing the variance of sensory distributions.
Key words: Sensory evaluation, difference tests, Thurstonian models, signal detection theory, cognitive strategies.
Unidad de Investigación y Desarrollo en Alimentos, Instituto Tecnológico de Veracruz, Veracruz, México.
Department of Food Science and Technology University of California, Davis, California, E.E.U.U.
La ciencia progresa a través del desarrollo de teorías y modelos. Hasta hace poco, la ciencia sensorial de los alimentos se consideraba como una compilación de métodos sin fundamento teórico. Se asumía que sí el análisis estadístico de los datos era suficientemente sofisticado, esto compensaría por los problemas asociados con las mediciones sensoriales. Sin embargo, esta suposición no es válida. Independientemente de lo sofisticado del análisis estadístico, nada puede hacer que los defectos en las mediciones sensoriales inapropiadas desaparezcan. Recientemente, este error se ha puesto de manifiesto. Los investigadores han reconocido que las mediciones sensoriales presentan problemas por lo que el énfasis hoy en día es en la aplicación de modelos a la metodología sensorial. El modelo más avanzado, a la fecha, es el de Thurstone.
El modelo de Thurstone fue originalmente aplicado a las pruebas de diferencia. Estas últimas permiten determinar el grado de diferencia o la magnitud de la diferencia entre dos estímulos confundibles, los cuales son tan parecidos que resulta difícil considerarlos como iguales o diferentes. Este tipo de mediciones sensoriales son importantes en estudios sobre vida útil, reformulación de producto, tipo de empaque, cambio de proceso de producción, etc., así como en programas de control de calidad y desarrollo de nuevos productos.
Las pruebas de diferencia no presentan la misma sensibilidad (1-16). Las investigaciones pueden resultar mostrando diferencias con una metodología y falta de diferencia con otra metodología sensorial. Hay varios reportes donde se compara el desempeño de los jueces utilizando varios protocolos sensoriales para evaluar diferencias. Fue precisamente esta discrepancia en los resultados que propició el desarrollo de teorías y modelos.
Como primer intento, se ha aplicado el modelo Thurstoniano (17,18) y la teoría de detección de señales (19, 20). El modelo Thurstoniano fue originalmente aplicado en las pruebas triangular, dúo-trio y comparación por pares o 2-AFC (prueba de selección forzada de dos alternativas por sus siglas en ingles, (2-Alternative Forced Choice) (21). Posteriormente, se han desarrollado modelos univariados y multivariados para otras pruebas de diferencia (22-47). Estos modelos han permitido el cálculo del parámetro d’ (d prima), que es el índice Thurstoniano de grado de diferencia. El cálculo se realiza a partir de la proporción de respuestas correctas obtenida en la prueba de diferencia correspondiente. Los modelos desarrollados hicieron posible el desarrollo de tablas que relacionan la proporción de respuestas correctas y el parámetro d’ (21, 34,48-52), y dicho modelo y sus aplicaciones se han discutido ampliamente (24, 53-56). La comprensión del modelo se facilita al entender los conceptos de la variabilidad de la percepción sensorial y el índice de discriminación, denominado parámetro d’.
El modelo de Thurstone se basa en dos suposiciones: la variabilidad de la percepción sensorial y el establecimiento de la estrategia cognitiva propia de cada prueba sensorial. Para explicar el significado de la primera suposición debemos imaginar la degustación de estímulos. Al evaluar sensorialmente un estímulo ‘X’, todas las sensaciones emanadas de la degustación del estímulo son enviadas al cerebro a través del sistema nervioso, pero las sensaciones no son constantes. El sistema nervioso presenta fluctuaciones en el número de nervios estimulados por la sensación y por la intensidad de la sensación derivada de la degustación. Esto es el resultado de las diferentes interacciones que tienen lugar en la boca. El sabor del estímulo se diluye con los fluidos orales, que incluyen la saliva que se secreta a diferentes velocidades y la presencia de residuos de la degustación previa. El sistema gustativo se torna insensible a la presencia de estos componentes de tal manera que la intensidad de la degustación y la estimulación transmitida al cerebro varía. Además, el mismo estímulo puede ser heterogéneo, lo que aumenta la variabilidad a la estimulación nerviosa. Así, algunas degustaciones resultarán más intensas y otras menos intensas. Pero, la intensidad promedio de la degustación será la que se presente con mayor frecuencia. La frecuencia con que aparecen las diferentes intensidades de percepción del estímulo puede representarse a través de una distribución normal de frecuencias. La aplicación de la primera suposición del modelo Thurstoniano es la representación de la distribución de la intensidad de la percepción sensorial del estímulo. Al evaluar un segundo estímulo ‘Y’ diferente al primero, la intensidad de la percepción se espera sea diferente. El nuevo estímulo aumentará la cantidad de estimulación transmitida al cerebro de tal manera que en términos de la distribución de frecuencias puede verse como una nueva distribución con intensidades más altas. El juez puede fácilmente discriminar entre un estímulo y otro, las dos distribuciones de frecuencia son perceptiblemente diferentes.
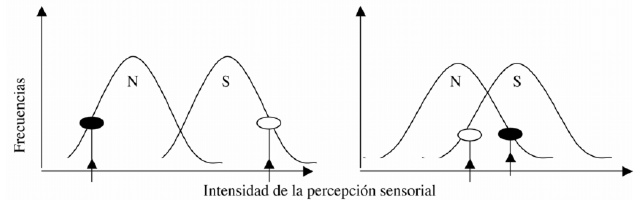
Sin embargo, al comparar dos estímulos ligeramente diferentes, las distribuciones de frecuencia se sobreponen entre sí y los estímulos serían confundibles. En el nivel alto de intensidad de la percepción, el estímulo se identificaría como ‘Y’, en intensidades bajas se identificaría como ‘X’. En intensidades promedio, en donde las distribuciones se sobreponen, los estímulos se percibirían a veces como ‘X’, a veces como ‘Y’, sería difícil identificarlos correctamente. Evidentemente que entre más separadas se representen las dos distribuciones de frecuencia de percepción, más fácil será discriminarlos. Así, el nivel de separación de las distribuciones puede utilizarse como una medida de que tan bien los jueces discriminan entre los dos estímulos. La distancia entre las medias de cada una de las dos distribuciones constituye el parámetro de d’; es un término adoptado por ingeniería de comunicaciones. Entre más grande es el valor de d’, mayor es el grado de diferencia entre los estímulos. La distancia entre las medias se mide en unidades de desviación estándar. Así, cuando el valor de d’ es igual a 1.5 implica que las distribuciones de intensidad de percepción de los estímulos se encuentran separadas por una distancia de 1.5 desviaciones estándar. Prácticamente d’ es una medida de la diferencia entre dos estímulos en términos de la variabilidad del estímulo. Para un ingeniero de comunicaciones es equivalente a la relación señal-ruido.
La variabilidad de la percepción sensorial de acuerdo al modelo Thurstoniano puede representarse en una distribución normal (Figura 1). Dicho modelo provee mayor información al comparar la varianza de las distribuciones de la percepción sensorial de los productos evaluados. De acuerdo a las distribuciones respresentadas en la Figura 2, la unidad de medida de d’ es la desviación estándar. Si la desviación estándar aumenta, el valor de d’ disminuye. Así, para una desviación estándar igual a uno, el valor de d’ puede ser igual a dos. Si la desviación estándar se duplica, la unidad de medición también se duplica y el valor de d’ se reduce a la mitad. Cualquier variable experimental que presente desviaciones estándar o varianza elevada, reducirá el valor de d’. ¿Cuáles son estas variables que incrementan la varianza? En primer lugar, el grado de reacción al estimulo del sistema gustativo puede asumirse como la principal causa que genera la diferencia de percepción entre las dos distribuciones. Jueces con mayor variabilidad en el sistema nervioso, debido a fluctuaciones grandes en la velocidad de activación del sistema nervioso no relacionada con la presencia del estimulo bajo evaluación si no que sólo son estimuladas espontáneamente, presentará una distribución con varianza más grande.
Como resultado, el valor de d’ disminuye. Otra forma de expresar lo mismo es decir que para que dos productos se perciban como diferentes, éstos deben presentar diferencias mayores a la variabilidad aleatoria en el sistema sensorial para un producto dado.
En segundo lugar, las diversas interacciones que ocurren en la cavidad oral también contribuyen en la varianza de manera importante. A mayor varianza, más difícil le resulta al juez detectar diferencias entre los productos a evaluar. De igual manera, si los productos presentan variabilidad en sí mismos, debido a la mala calidad, será más difícil para el juez percibir las diferencia entre los productos. Así, las diferencias entre los productos deben ser superiores a la variabilidad de los mismos productos para reportar diferencias.
Otra fuente de variación es el resultado de la secuencia de las degustaciones de los estímulos. Por ejemplo, al degustar un alimento, seguido de otro alimento de intensidad similar o más intenso al primero, la insensibilidad provocada por el remanente de la primera degustación hará que el segundo alimento se perciba menos intenso de lo que debiera. El efecto será inverso si la secuencia de las degustaciones cambia. Sin embargo, un aumento de la salivación, en la expectoración o en la deglución disminuirá el efecto. De cualquier manera, el efecto estará más o menos presente, aumentando la variabilidad en la distribución (31, 60-63, 65-73).
El efecto de la memoria y el olvido añaden variabilidad a la distribución de percepción de los productos. Las pruebas de diferencia involucran comparar el sabor de un alimento con el recuerdo del alimento previamente degustado. Mientras más tiempo pasa entre las degustaciones, menos preciso será la variabilidad asociada a la memoria del alimento degustado previamente. Este aumento en la variabilidad producirá una reducción en el valor de d’, lo cual predice que las pruebas de diferencia con tres muestras son menos discriminatorias que las de dos estímulos (13,71,72-76).
No es fácil entender el concepto de d’ sin antes usarlo. A fin de tener una idea de lo que representa, es útil saber que cuando d’ es igual a uno representa la diferencia entre dos estímulos que apenas se perciben como diferentes. La magnitud de la diferencia se dice que está en el umbral de percepción. El concepto se comprende mejor a través de un ejemplo en donde se aplica la prueba de diferencia de comparación por pares.
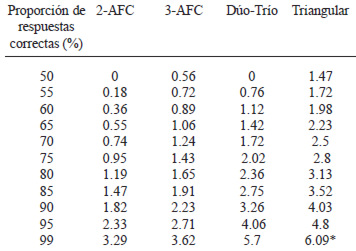
Imaginemos la situación en la que a un juez se le pide que identifique, entre dos muestras, la que percibe con mayor intensidad en dulzor. Si el juez discrimina fácilmente entre las dos muestras, todas las pruebas de comparación por pares serán correctas (100% de respuestas correctas). Si el juez no discrimina entre las muestras, su respuesta será aleatoria y obtendrá 50% de respuestas correctas. Cuando obtiene 75% de respuestas correctas se encuentra en el umbral de percepción de la diferencia; es decir entre discriminación total (100% de respuestas correctas) y respuesta aleatoria (50% de respuestas correctas). El valor de d’ igual a uno corresponde al 76% de respuestas correctas en una prueba de comparación por pares. El cálculo de d’ toma en cuenta las suposiciones del modelo de Thurstone (49). La Tabla 1 presenta algunos ejemplos de la relación entre el valor de d’ y la proporción de respuestas correctas para diferentes pruebas de diferencia.
A través de la Figura 1 se puede presentar un ejemplo de la aplicación del modelo. Dicha figura representa las distribuciones de frecuencia de percepción de intensidades de dos estímulos confundibles, pues las distribuciones se sobreponen. Suponiendo que N representa el estímulo menos intenso y S representa el estímulo más intenso; cuando el juez degusta cualquier estímulo lo puede percibir en un nivel de intensidad cualquiera de la distribución correspondiente. La tendencia más frecuente es que se perciba a un nivel promedio de intensidad en donde la frecuencia es más alta. Si nos imaginamos que la intensidad del estimulo N, representada por el óvalo negro, se percibe en un nivel bajo de intensidad y que cuando el juez degusta el estimulo S, representado por el óvalo blanco, lo percibe a un nivel de intensidad alto, al contestar la pregunta de cuál de los dos estímulos es más intenso en dulzor, indicará el estímulo S, y se le calificaría correctamente (Figura 1, lado izquierdo). Al considerar nuevamente la figura 1, en esta degustación el sistema nervioso esta un poco más activo de tal manera que al degustar el estimulo N, lo percibe a un nivel más alto de intensidad del atributo (óvalo negro). Por otro lado, al degustar el estimulo S, el sistema nervioso se encuentra en un nivel de estimulación bajo, de tal manera que el nivel de intensidad de percepción se encuentra en la parte menos intensa de la distribución S (óvalo blanco). Si le pregunta sobre cuál de los dos estímulos es más intenso en dulzor, elegirá el estimulo N, dando un resultado incorrecto (Figura 1, lado derecho). Así, algunas veces el juez acierta en su respuesta, otras no. Esta es la situación durante la degustación de estímulos confundibles que normalmente son evaluados por pruebas de diferencia. Entre más se sobreponen las dos distribuciones (menor valor de d’), mayor la probabilidad de error de los jueces. Al repetir este mismo ejercicio 100 mil veces a través de modelo de simulación Monte Carlo, se estimaría la proporción de veces que la prueba de comparación por pares se acierta para un valor de d’ en particular. Este mismo ejercicio se repetiría para toda una serie de valores de d’. Lo que daría origen a una tabla en donde se relacionan la proporción de respuestas correctas y el valor de d’ (49).
Este mismo ejercicio puede representarse para las diferentes pruebas de diferencia, dando como resultado tablas que correlacionan la proporción de respuestas correctas con el valor correspondiente de d’. Esto quiere decir que las pruebas de diferencia como la prueba de comparación por pares y la prueba triangular pueden comparase directamente aún cuando la probabilidad de respuesta al azar de ambas pruebas es diferente. El parámetro d’ permite la comparación de pruebas de diferencia con probabilidades de respuesta aleatoria diferentes, algo que no se podría hacer al aplicar el modelo binomial. Por lo tanto, d’ es una medición básica, fundamental pues es independiente de la metodología aplicada.
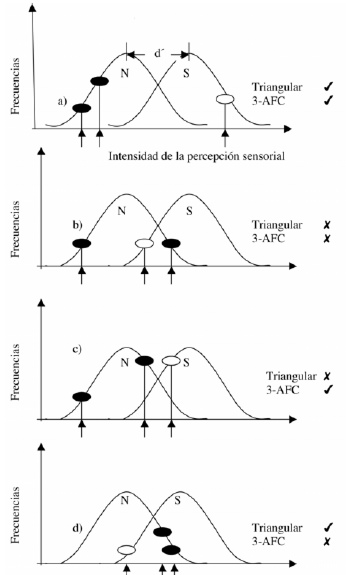
Al aplicar las diferentes pruebas de diferencia para evaluar el mismo par de estímulos, algunas pruebas permiten discriminar mientras que con otras no se reportan diferencias entre los estímulos. Esta paradoja de resultados puede ejemplificarse a través de las pruebas triangular y 3-AFC (Figura 3).
En la prueba triangular se presentan tres estímulos al juez; en donde dos de las muestras corresponden al mismo estímulo y una muestra corresponde al otro estímulo (muestra diferente). La tarea del juez es degustar las tres muestras e identificar la muestra que es diferente. En la prueba 3-AFC (3-alternative forced choice), la tarea es ligeramente diferente. El juez degusta las tres muestras pero ahora se le indica el atributo en el que difieren las muestras. El juez debe identificar la muestra con mayor intensidad en el atributo a evaluar. Por ejemplo, al evaluar la acidez en dos muestras de café usando la prueba 3-AFC, el juez degusta las tres muestras y se le pide identificar la muestra de café con mayor intensidad en acidez. Los resultados de la aplicación de las pruebas triangular y 3-AFC reportan mejor desempeño de los jueces cuando utilizan la prueba 3-AFC. Esta diferencia en el desempeño de los jueces se reportó por primera vez en 1937 por Abrahams y colaboradores (57) y durante muchos años no se pudo explicar. Años más tarde, se le conoció como la paradoja de las pruebas de diferencia (discriminatorias y no-discriminatorias) (8). Es posible que se atribuya el mejor desempeño de la prueba 3-AFC al hecho de que el juez conoce el atributo a evaluar. Sin embargo, ésta no es la explicación. Hay otras pruebas sensoriales en donde el juez se desempeña mejor cuando desconoce el atributo que cambia (58). No fue sino hasta 1979 que Frijters (35, 36) encontró la solución a la paradoja, a través de los conceptos del modelo de Thurstone. La solución es la siguiente.
Si se considera nuevamente los estímulos N y S de la Figura 2, siendo dos estímulos del tipo N y un estímulo del tipo S, ligeramente más intenso. Los dos estímulos denotados con los óvalos negros pertenecen a la distribución del estímulo N, mientras que el óvalo blanco pertenece a la distribución del estímulo S. Al considerar la parte superior de la Figura 2 (Figura 2a), se observa que los dos estímulos (óvalos negros) se encuentran en la parte central y baja de la distribución N, el estimulo de mayor intensidad S, se denota por el óvalo blanco. Al aplicar la prueba triangular, el juez deberá identificar la muestra diferente y elegirá el estímulo S, pues es el más alejado de los dos estímulos representados por los óvalos negros. Al aplicar la prueba 3-AFC, deberá identificar la muestra más intensa y elegirá el estímulo S, pues es el más alejado a la derecha en el eje de intensidad de percepción. De tal manera que en este ejercicio en ambas pruebas se reportan respuestas correctas.
Al considerar las distribuciones de la Figura 2b, se observa que un estímulo se asocia con la parte izquierda de menor frecuencia de la distribución N y el otro se localiza en la parte cercana a la frecuencia más intensa. El estímulo S por otro lado, se localiza en la parte más baja de intensidad de su distribución; en realidad se localiza a un nivel de intensidad más bajo que uno de los estímulos N. Al aplicar la prueba triangular, el juez elegirá la muestra más alejada y en este caso será el estímulo negro de la izquierda de la distribución N. Con la prueba 3-AFC, al identificar la muestra de mayor intensidad de percepción, elegirá el estímulo más alejado en el eje de intensidad, es decir el estímulo del óvalo negro. En ambos casos, la respuesta es incorrecta. Sin embargo, el error no es el mismo. Las pruebas sensoriales triangular y 3-AFC no son equivalentes.
Al considerar las distribuciones de la Figura 2c, uno de los estímulos representados con los óvalos negros se localiza en la parte baja en intensidad de la percepción del estímulo N y el segundo se localiza en la parte alta de la distribución. El estímulo S (óvalo blanco), ubica la intensidad de percepción en la parte baja de la distribución. Con la prueba triangular, el juez identificará el estímulo N ubicado en la parte baja de la distribución como la muestra diferente, pues es la muestra más alejada de las otras dos. Desde luego que esta respuesta es incorrecta. Con la prueba 3-AFC, el juez identificará la muestra S como la muestra de mayor intensidad de percepción, pues es la muestra más a la derecha en el eje de intensidad del atributo. Esta respuesta es correcta. Es así que a partir de la misma información que el cerebro recibe de los sentidos, el juez toma una decisión correcta con la prueba 3-AFC e incorrecta con la prueba triangular. Sin embargo, la sensibilidad del juez es la misma. Esta discrepancia en los resultados se debe a que el juez realiza la toma de decisión de manera diferente en cada prueba. El proceso de toma de decisión con la prueba 3-AFC es más eficiente.
Finalmente, al analizar la Figura 2d se observa que los estímulos están totalmente intercambiados. Este suceso es raro. Sin embargo, en esta situación la prueba triangular resultaría correcta y la 3-AFC incorrecta.
Al modelar estos escenarios con estímulos que presentan grado de discriminación correspondiente al valor de d’ igual a uno y para una muestra de 100 000, el escenario ilustrado en el caso (a) aparece 37% de las veces; el caso (b) ocurre 32% de las veces; el caso (c) aparece 26% de las veces, y el caso (d) ocurre 5% de las veces. Así, paraestímulos con el mismo grado de discriminación (igual valor de d’), el desempeño de la prueba 3-AFC será superior al de la prueba triangular. La explicación teórica de Frijters’s (35), sobre la paradoja de las pruebas de diferencia, hizo necesaria la confirmación experimental. Fue necesario demostrar experimentalmente que para el mismo grupo de jueces que degusta el mismo par de estímulos reporta proporción de respuestas correctas mayores utilizando la prueba 3-AFC que con la prueba triangular (59-63). Por ejemplo, para d’ igual a uno, se espera 42% de respuestas correctas con la prueba triangular y 63% de respuestas correctas con la prueba 3-AFC.; para d’ igual a dos, la proporción de respuestas correctas será 60 y 87%, respectivamente. Estos valores están disponibles en tablas que relacionan la proporción de respuestas correctas con el valor de d’ para cada prueba de diferencia (49). Es interesante recordar que la probabilidad de respuesta al azar en ambas pruebas es la misma: 33.33%. Las pruebas estadísticas que se basan en la probabilidad de respuesta al azar como la prueba binomial y ÷2 no consideran el desempeño superior de la prueba 3-AFC con respecto a la prueba triangular. El análisis basado en el modelo de Thurstone y el calculo de d’ es más revelador. La significancia estadística de d’ también puede estimarse (64).
La prueba de comparación por pares y la prueba dúo-trio también pueden modelarse de la misma manera. En éstas, el desempeño de la prueba de comparación por pares es superior al de la prueba dúo-trio, aun cuando el valor de d’ es el mismo. Así, para muestras con valor de d’ igual a uno, se espera 58% de respuestas correctas con la prueba dúo-trio y 76% con la prueba de comparación por pares. Para d’ igual a dos, la proporción de respuestas correctas será 75% para dúo-trio y 92% para comparación por pares.
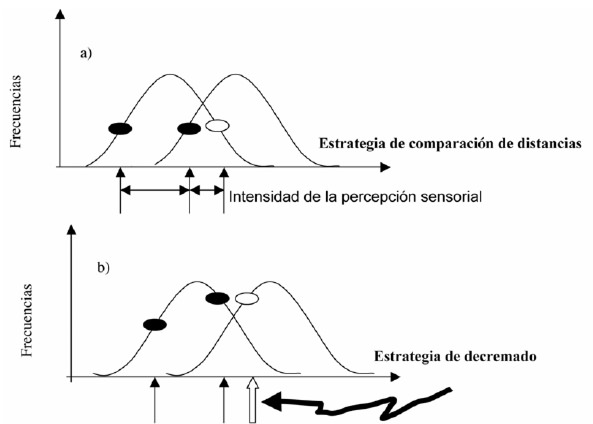
¿Porqué la prueba 3-AFC y la prueba de comparación por pares permiten un desempeño superior en los jueces? La explicación se resume a través de las estrategias cognitivas que utiliza el juez en las pruebas triangular y 3-AFC (Figura 3). En la prueba triangular, el juez ubica la muestra diferente como la que más se aleja de las otras dos muestras. Esta tarea la realiza comparando las distancias entre los estímulos en el eje de intensidad de la percepción. Esta estrategia se denomina ‘comparación de distancias’ (Figura 3). En la prueba dúotrio, los jueces también aplican la estrategia de comparación de distancias.
En la prueba 3-AFC, el juez elige la muestra de mayor intensidad de percepción. Esta estrategia se conoce como ‘descremado’ porque el estímulo de mayor intensidad es eliminado de la misma manera que se elimina la espuma de la cerveza (Figura 3). La prueba de comparación por pares utiliza la estrategia cognitiva de descremado. En el análisis de la Figura 3 se observa que la estrategia de descremado es más eficiente que la de comparación de distancias.
Cuando estos principios no se comprenden, se puede llegar a conclusiones erróneas. Si un panel reporta 90% de respuestas correctas en la prueba de comparación por pares puede concluirse que la diferencia entre los productos evaluados es más grande que la diferencia reportada por un panel con 80% de respuestas correctas usando la prueba dúo-trio. Estadísticamente hablando, esta conclusión es lógica pues ambas pruebas tienen la misma probabilidad de respuesta al azar. Sin embargo, la prueba de comparación por pares opera con la estrategia de descremado (más eficiente) y la dúo-trio con la estrategia de comparación de distancias (menos eficiente). Para que la prueba dúotrio resulte en un 80% de respuestas correctas, la diferencia entre las muestras, estimada por el parámetro d’, deberá ser igual a 2.36. En la prueba de comparación por pares, 90% de respuestas correctas, corresponde a una diferencia entre los estímulos de 1.82. En consecuencia, a pesar de lo esperado estadísticamente con la probabilidad de respuesta al azar, la diferencia estimada con la prueba dúo-trio es mayor que la estimada con la prueba de comparación por pares.
La potencia estadística de una metodología se entiende como la capacidad para reportar diferencias cuando estas existen. La eficiencia de las estrategias cognitivas de las pruebas de diferencia puede ilustrarse a través de la potencia estadística. Los resultados de la medición indican que para un valor de d’ igual a uno, 5% de significancia estadística y con 90% de potencia (capacidad de detectar diferencias 90% de las veces), la prueba 3-AFC requiere 21 comparaciones para declarar diferencias mientras que con la prueba triangular requiere 276 evaluaciones. El número de evaluaciones requeridas para la prueba de comparación por pares y dúotrio es 27 y 310, respectivamente. Estos valores claramente ilustran la diferencia masiva en potencia estadística entre las pruebas sensoriales que aplican la estrategia de descremado y la estrategia de comparación de distancias.
El modelo Thurstoniano permite comprender las bases de las pruebas discriminatorias o de diferencia. Uno de los aspectos más relevantes puede ser la variabilidad de la percepción de los estímulos. Es decir, un alimento que se degusta de manera rápida y repetitiva no se percibe exactamente con la misma intensidad en cada degustación. La variabilidad en la percepción sensorial constituye el principal fundamento del modelo Thurstoniano. Este supuesto provee de una medición básica de la diferencia entre dos estímulos confundibles a través del parámetro d’ (d prima), que es independiente de la prueba de diferencia utilizada. La capacidad para determinar mediciones básicas o fundamentales es esencial para cualquier disciplina científica. Las mediciones de desempeño, como la proporción de respuestas correctas no son independientes de la metodología sensorial. El desempeño del juez con la prueba 3-AFC es mejor que con la prueba triangular, mientras que la sensibilidad (d’) para ambas pruebas es la misma. Finalmente, la consideración de la varianza de las distribuciones permite explicar las variables experimentales asociadas a la memoria y la secuencia de las degustaciones.
Los ejemplos de las distribuciones mencionados son univariados y tienen que ver con pruebas de diferencia. Pero los mismos conceptos aplican para mediciones de intensidad con escalas, para pruebas de diferencias multivariadas, para estadística multivariada o para mapeo de productos. El modelo de Thurstone es una estructura poderosa para entender los mecanismos de la medición sensorial.
Recibido: 10-12-2008
Aceptado: 12-05-2009